di Paolo Reale
Spesso nei casi giudiziari c’è la necessità di valutare delle misure relative alle dimensioni di oggetti o persone inquadrate, tuttavia a volte – per diversi motivi – non è possibile applicare i metodi di elaborazione delle immagini tramite software, oppure le immagini disponibili non sono state pensate per questi scopi, ma rimangono comunque le uniche testimonianze utili.
Se è vero che, grazie a tablet, smartphone, e alle reti dati fisse e mobili di nuova generazione, la società attuale è considerata “iperconnessa”, per ragioni analoghe è di fatto anche molto più “multimediale”. Del resto una telecamera o fotocamera, peraltro di buona (se non ottima) qualità, è di fatto sempre in tasca a disposizione per ogni situazione: dalla foto più frivola del piatto di portata del ristorante alla moda, alla video-documentazione di un fatto di cronaca rilevante in cui si rimane casualmente coinvolti. Per non parlare del fronte della videosorveglianza in cui si possono apprezzare significative evoluzioni: ormai l’indagine di molti crimini, specie nelle fasi iniziali, si appoggia sui riscontri che pervengono dalle immagini delle telecamere dislocate negli esercizi commerciali come nei luoghi pubblici, di qualità sempre migliore e (soprattutto) sempre più numerose.
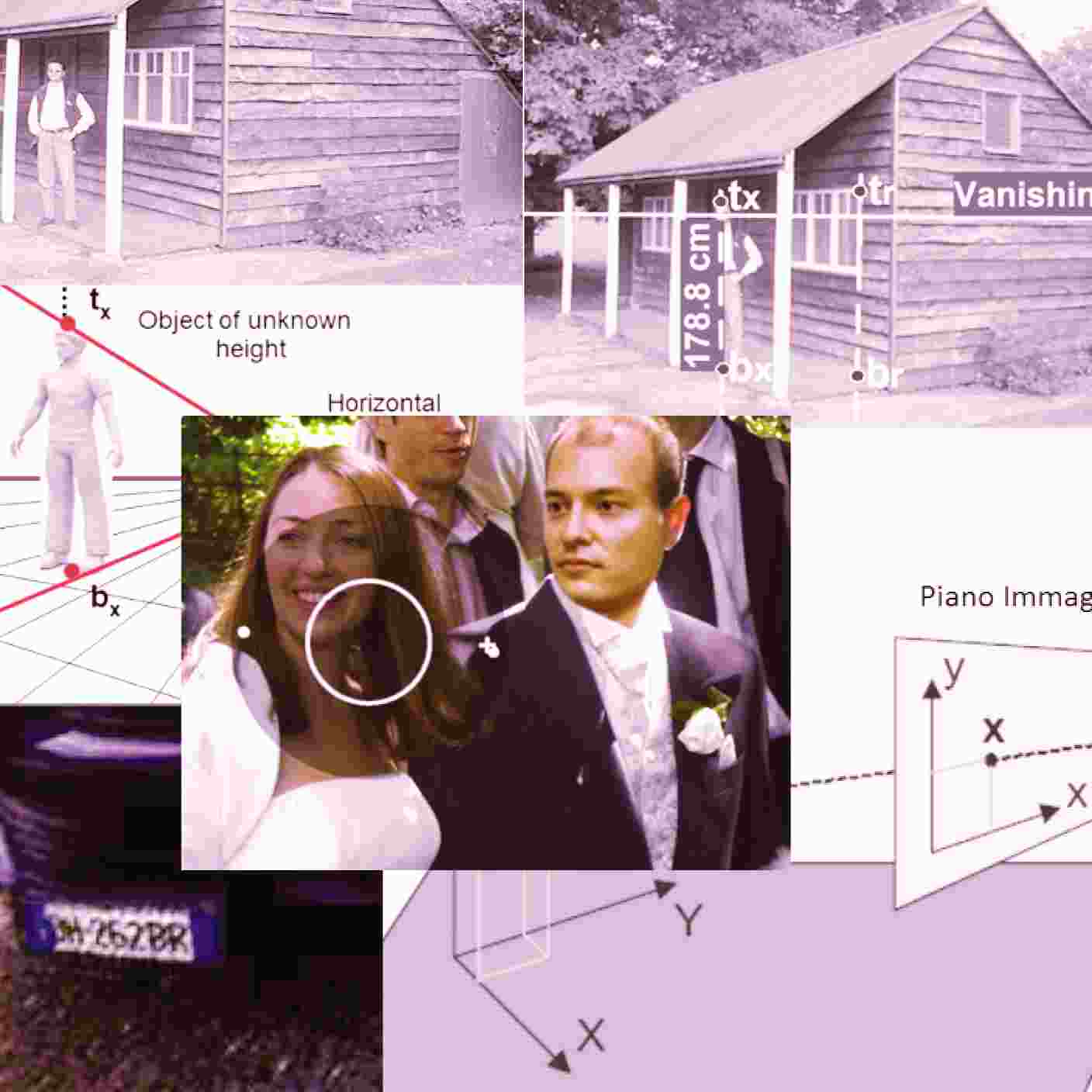
Da questi elementi deriva poi il fatidico problema di rilevare le misure “reali” di qualcosa o qualcuno (un’altezza, una lunghezza, etc.), partendo dalla foto, o fotogramma, che purtroppo di dimensioni ne ha due, e a seconda della prospettiva o dell’inquadratura può riservare notevoli difficoltà. Esistono diversi approcci che possono consentire di realizzare comunque una stima della misura cercata, ognuno dipendente dalla particolare situazione in cui ci si trova. Uno di questi, tra i più tipici al fine di poter effettuare delle misurazioni ‘reali’ sulle fotografie laddove si hanno dei riferimenti architettonici come riferimento, è quello di effettuare opportune operazioni di trasformazione dell’immagine di tipo matematico (trasformazioni omografiche), denominate di “raddrizzamento fotografico”. Senza pretesa di esaustività sull’argomento, l’obiettivo della trasformazione è quello di eliminare ogni effetto prospettico consentendo di rilevare le informazioni metriche.
Nel caso di una telecamera di sorveglianza fissa, si può arrivare a ottimi risultati anche attraverso la ricostruzione nella realtà della situazione presente nel fotogramma: in altre parole si posizionano le persone o gli oggetti, di cui si cercano le dimensioni (p. es. un’autovettura), in modo identico a quello registrato nel fotogramma, e rivedendo la scena così ripresa dalla telecamera. Per quanto non sia utilizzata con frequenza, questa modalità ha il pregio di consentire una sorta di replicabilità dell’approccio senza introdurre errori nelle trasformazioni matematiche.
Fermo restando il fatto che, al di là degli approcci possibili, esistono numerose casistiche per le quali non è possibile pervenire ad alcun risultato, per diverse ragioni (p.es. l’immagine non presenta riferimenti utili di nessun tipo, non è nota l’ottica né la prospettiva di scatto, etc.), è utile valutare se si può arrivare quantomeno ad una valutazione (stima) di misura con un approccio statistico, sempre grazie alla presenza di qualche elemento di cui si ha nota a priori la dimensione.
A volte infatti, specie nelle fotografie scattate per esigenze di repertamento sulle scene del crimine, si può trovare un riferimento metrico, il classico “righello”, posizionato magari anche non in modo ottimale, ma comunque utile a rappresentare un elemento di confronto. La necessità dell’approccio statistico nasce per due esigenze: innanzitutto consentire di comprendere il livello di errore intrinseco nella misura effettuata, con cui necessariamente confrontarsi per ogni ipotesi di compatibilità; consentire la verifica, magari da più immagini, della stessa misura, tramite i test statistici che consentono di arrivare a comprendere la ‘compatibilità’ (sono statisticamente coerenti tra loro) nel confronto tra le diverse misure rilevate, oppure la loro ‘non compatibilità’ (le differenti misure si devono verosimilmente attribuire a due diverse dimensioni reali).
Per illustrare questo approccio si utilizzerà un esempio pratico, facendo prima una premessa metodologica sulla procedura da adottare.
L’approccio qui proposto per poter effettuare le misure su fotografie per le quali non si possono adottare altri sistemi, si basa sulla determinazione di un insieme di punti campione collocati sia lungo il righello di riferimento che sulla traccia da misurare.
Detti punti, all’interno del piano dell’immagine, avranno necessariamente delle coordinate cartesiane esprimibili (come unità di misura) in pixel. In pratica, ogni punto P potrà essere individuato come P(x,y), cui x sarà la coordinata orizzontale espressa in pixel e y la coordinata verticale espressa in pixel. È quindi possibile calcolare la distanza geometrica tra i punti utilizzando le normali formule di distanza cartesiana (o teorema di Pitagora). Definendo due punti P1(x1,y1) e P2 (x2,y2), la distanza tra i due punti sarà:
Si noti che, una volta ottenute le due sequenze di misure lungo le due direttrici (righello e segno), il loro rapporto consentirà di trasformare le misure di dette distanze in metriche: poiché i campioni sul righello verranno individuati per ogni millimetro, il rapporto tra le distanze (espresse in pixel) dei segni e il righello, darà una misura espressa in millimetri. Ottenute le misure, in millimetri, delle distanze tra i singoli punti di interesse, sarà possibile fare alcune valutazioni statistiche, in particolare calcolare la media e gli altri parametri della distribuzione normale (o gaussiana), quali varianza e deviazione standard.
Seguendo questo approccio sarà quindi possibile ottenere i valori di distanza medi (e gli altri parametri statistici), in questo caso esemplificativo analizzato più avanti (si veda la fotografia) il ‘passo’ tra i denti della cerniera zip. Queste misure, messe a confronto su più fotografie, possono consentire di fare una valutazione – sempre sotto il profilo statistico – se sono effettivamente considerabili come “compatibili” oppure no. Per questa valutazione, poiché si tratta di mettere a confronto dei valori medi (per i quali conosceremo anche gli altri parametri statistici), è possibile utilizzare il test t (o test di student).
Detto test è utilizzato per poter rispondere alla domanda: “la differenza fra le medie dei due campioni è significativa?”. Oppure, in altri termini: è possibile affermare che la differenza osservata non è dovuta al caso ma che, invece, esiste veramente una diversità tra le medie delle due misure da cui i campioni stessi derivano?
Il procedimento statistico che viene utilizzato consiste nel valutare la cosiddetta “ipotesi zero”, ovvero si parte dall’ipotesi (denominata H0) in cui i dati provengono dallo stesso insieme, per cui la differenza tra i valori medi misurati non sarebbe realmente significativa di due insiemi diversi, ma sarebbe attribuibile al caso (o l’errore) con il quale vengono prelevati i campioni. Il test t consente di rispondere alla domanda se sia possibile accettare l’ipotesi H0 oppure se va rifiutata.
Ovviamente, si tratta di una valutazione statistica: il test di significatività non fornisce una prova di assoluta certezza, ma si limita a fornire un’indicazione della forza con cui i dati contrastano l’ipotesi zero. In altre parole, la decisione presa nel test di respingere l’ipotesi zero è “probabilmente” giusta, e l’errore che si può commettere in questa decisione è esprimibile “livello di significatività del test”.
Un esempio pratico
Riassumendo, quindi, ed esemplificando sulla foto accanto, che per ovvie ragioni non potrà mai essere ‘raddrizzata’ tramite le citate tecniche di trasformazione. Si prendono i punti ‘campione’ lungo le direttrici del riferimento metrico e della cerniera ‘zip’. Applicando le formule della distanza tra due punti è possibile calcolare tutte le distanze tra i punti, e rapportandole tra loro ottenere una misura metrica media, e la sua varianza e deviazione standard.
Non si farà in questa sede, ma è chiaro che applicando lo stesso approccio su un’altra foto degli stessi oggetti sarà possibile ottenere un altro set di misure: valor medio, varianza e deviazione standard. Una semplice “prova del 9”, al fine di verificare se le due medie così calcolate (con i relativi parametri statistici) possano essere effettivamente coerenti tra loro, può essere fatta procedendo con il metodo del test t. Sapendo che entrambe le misure effettuate provengono dallo stesso oggetto reale, tramite due diverse rappresentazioni fotografiche, ci chiediamo se queste due medie calcolate, differenti tra loro, possano essere comunque effettivamente attribuibili allo stesso insieme di partenza, tramite il test di student.
Il risultato ottenuto ci consente di affermare che “con elevata probabilità”, o comunque commettendo un errore dell’ordine di meno dell’1%, le due medie calcolate sono riferibili allo stesso oggetto, fornendo quindi una maggiore solidità alla misura presa. In modo del tutto analogo, si possono pensare confronti orientati a capire se effettivamente due oggetti diversi hanno misure differenti tra loro o meno. L’aspetto di sicuro interesse di un metodo come questo è che consente di ottenere senza troppe difficoltà le stime cercate, corredate dalla possibilità non solo di definire un margine di errore, di grande importanza in ambito forense, ma anche la possibilità (attraverso i confronti tra set di misure differenti, provenienti da ulteriori immagini) di consolidare l’attendibilità di questi risultati.©